17

Is −9 a smaller number than −8?

And is −9 a lower number than −8?

What is the difference between lower and smaller here?

RegDwigнt
  • 97,231
Johannes Schaub - litb
  • 857
  • 5
  • 9
  • 18
  • 1
    I remain of the opinion that – swanky graphics notwithstanding – the opinion of an octagenarian maths teacher should not be the deciding factor in establishing what if any difference there is between smaller and lower in this very precise context. – FumbleFingers Jun 23 '11 at 02:34
  • 1
    @Fumble I agree. The NGram diagrams are telling a different picture here. I will unaccept the answer and when I have more time I will see what answer I finally accept. – Johannes Schaub - litb Jun 23 '11 at 09:52

6 Answers6

11

My gut instinct as a PhD mathematician is that −9 is lower than −8, but not smaller than −8.

There is not a technically correct term without more context being given. If you are talking about the integer numbers (including positive and negative numbers) then I wouuld prefer to say that -9 is lower than -8. If you are talking about the magnitude of the numbers, rather than their place on the integer number line, then -8 is smaller and lower than -9 (although I would prefer to say smaller). As there is not a technically correct answer, these phrases are often used interchangeably in practice. Mathematical notation, such as -9<-8 and |-8|<|-9|, would need to be used to avoid misinterpretation.

"Less than" is also a good alternative phrase. It is the words intended by the < sign.

In summary, I would say that a small number is close to 0 and, in a context where negative numbers make sense, a low number is close to minus infinity. It is best to give more context of what kind of numbers you are talking about.

Chogg
  • 263
  • This answer can be improved by adding citations: reliable facts and references which show that the answer is correct. "As a PhD mathematician" is a good start. – MetaEd Sep 19 '12 at 17:38
  • 2
    @ΜετάEd Chogg speaks from an explicitly mathematical perspective; his degree, provides (for me at least) sufficient authority for his "technical" observations. This must be assumed to be pretty primitive stuff in his field. +1 A clear and subtle answer. – StoneyB on hiatus Sep 22 '12 at 04:03
  • Good point. I would never the less like to know a text which discusses this point. – Chogg Sep 08 '13 at 17:18
  • Good point. I would never the less like to know a text which discusses this point. A very early stage book on number theory might do it, but I don't know which. A reference to this ambiguity is given (again without reference) on http://en.wikipedia.org/wiki/Small_number. – Chogg Sep 08 '13 at 17:40
  • I just updated my answer to be clearer. – Chogg Sep 08 '13 at 17:50
  • 1
    @StoneyB: Mathematicians (also Engineers and other scientists) often need to distinguish between the magnitude of a number and the ordering of a number, and the comparison of these two quantities for different numbers. When making such a comparison, it has become usual to use the terms larger and smaller to refer to a comparison based on magnitude, and the terms higher and lower to refer to a comparison based on ordering. Often the two are the same, and no distinction is made, but where distinction is required, this agreement is commonplace in the technical community. continued ... – Pieter Geerkens Sep 08 '13 at 19:44
  • @StoneyB ... continuation. Here is a definition of smaller consistneet with this interpretation: https://www.google.ca/#q=definition+of+smaller, and here is a similarly consistent definition of lesser: https://www.google.ca/#q=lesser – Pieter Geerkens Sep 08 '13 at 19:47
  • 1
    @PieterGeerkens Interesting. Historians and archaeologists employ High for dates more remote from the present and Low for dates closer to the present. – StoneyB on hiatus Sep 08 '13 at 20:02
  • @StoneyB: That makes perfect sense to me, because the scale of interest is distance from the present, not distance from some indeterminate and uknowable point in the past. For archaeologists, it is also depth from ground level. – Pieter Geerkens Sep 08 '13 at 20:05
8

You can't argue with the whole English-speaking world, and the fact of the matter is they overwhelmingly prefer smaller to lesser or lower.

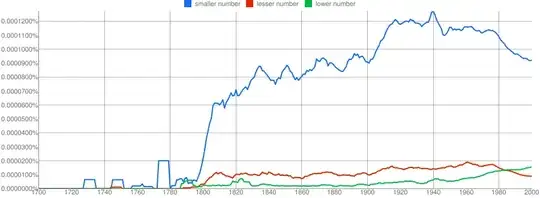
NGram usage

I think if pressed most people would agree that -1 is a 'bigger' number than -2. But negative numbers don't exactly have real-world correlates, so we all tend to be a bit vague on that one.

Even more vague - for those who know what imaginary numbers are - is the question of whether i is 'smaller' than 2i

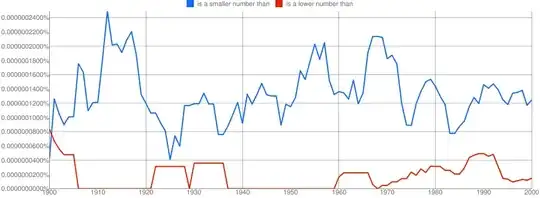
LATER: I have no opinion on whether either of OP's examples is more 'correct' than the other. They're both fine to me. I'm simply making the point that of the two specific usages being asked about, on average people prefer to use the former. Here's a somewhat more specific NGram for those who still want to dispute that point... ngram

FumbleFingers
  • 140,184
  • 45
  • 294
  • 517
  • thanks for your answer. what does the y-axis represent? – Johannes Schaub - litb May 22 '11 at 16:26
  • 2
    @Johannes Schaub - litb: Sorry, I should have said it came from NGrams. The y-axis is "frequency of occurence" as a percentage of the total number of words in the corpus (the millions of books indexed by NGram). So the more leading zeros you see, the rarer the search term is. But NGram always scales the y-axis for you. – FumbleFingers May 22 '11 at 16:45
  • @FumbleFingers: NGram is deceiving; lesser is non-grammatical or at least very uncommon in mathematics or everyday life as "less" already implies a comparison. See my edit. – Lie Ryan May 26 '11 at 04:51
  • 1
    @Lie Ryan: I see nothing deceptive there. I agreed in my comment against your answer that specialist contexts such as maths and computing normally use greater/less. It's hardly deceptive to point out that outside those specialist contexts people use smaller far more often than lesser. – FumbleFingers May 26 '11 at 13:25
  • @FumbleFingers: The problem is that "lesser" is used by neither mathematicians nor regular people; I'd probably argue that it's not even a word. The second problem is that you can construct any evidence on NGram by carefully choosing "less/lower/smaller", "less number/lower number/smaller number", "less than/lower than/smaller than", etc. Third, the OP italicized only the "lower" and "smaller" not "lower number" or "smaller number", therefore your interpretation of the question is not the privileged interpretation either. Lastly, "less number" is redundant as "less" usually implies numbers. – Lie Ryan May 26 '11 at 14:57
  • @Lie Ryan: Well strictly speaking the lesser of two evils would be for me not to reply to that at all, since you're obviously not going to be convinced whatever I say. – FumbleFingers May 26 '11 at 15:12
  • @FumbleFingers: Fair enough, lesser is a word; though I'm still not convinced that it is correct nor common to use lesser number than when comparing numbers. It is triple redundant. – Lie Ryan May 26 '11 at 15:28
  • 1
    @Lie Ryan: "Lesser number" is definitely used. It is not redundant at all - lesser is the comparative form of "little". – psmears Jun 21 '11 at 08:53
  • @psmears: ty for backup. I can't really see we're getting anywhere, because I can't actually make out what we're disagreeing about, so I don't know how to defend my point any more forcefully. Hey! - I don't even know what my point is! If you want to argue with people who think "lesser" might not even be a word, I've put the other one into "discussion". – FumbleFingers Jun 23 '11 at 02:30
  • Data is great, but this data doesn't pertain to negative numbers specifically, and that's what the poster is asking. – Michael Clerx Feb 07 '17 at 17:17
  • @Michael: Well, I did point out that negative numbers don't exactly have real-world correlates, so we all tend to be a bit vague on that one. Anyway, I only answered in the first place because I was seriously unimpressed with the accepted answer. Apart from the irrelevant business about font size, all it really says is: Don't use words at all (use the symbols > and <) - and that one doesn't even mention negative numbers at all. At least I broadened the scope to include imaginary numbers. – FumbleFingers Feb 09 '17 at 19:42
3

I would generally say that ‘bigger’ refers to magnitude (distance from zero) whereas ‘higher’ refers to value (distance from negative infinity), but in context anything is possible. We don't tend to use ‘big’ or ‘small’ in mathematical contexts very much. If you want to be correct, I would recommend ‘greater’ and ‘less’. In fact, the signs < and > are read ‘is less than’ and ‘is greater than’ respectively.

enter image description here
5 is smaller and lower than 3, but still greater.

Twey
  • 31
2

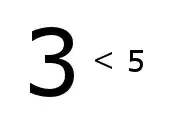
5 is smaller than 3

My math teacher used to say that in this inequality 5 is smaller than 3, but 3 is less than 5.

Joking aside, only less than and greater than are uniformly understood as < and > relation respectively; the other words (e.g. smaller, lower) are often used colloquially to mean less than, whose absolute values are less than, written smaller, etc however their usage are more ambiguous and so should be avoided when writing mathematics.

EDIT:

One could argue just about anything with Google NGram:

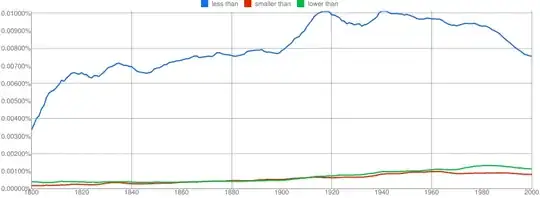
enter image description here

Lie Ryan
  • 834
  • 1
    @Lie Ryan: Definitely use greater/less when writing in a maths context, as you say. And computing, where it's common to write and even say LT/GT (even some computer languages themselves support these forms). But outside these specialist areas it's not just 'colloquial' to use smaller - it's overwhelmingly more 'standard'. – FumbleFingers May 22 '11 at 20:01
  • @Lie Ryan: re your recently-added NGram; OP's question isn't about the relative prevalence of less than, smaller than, and lower than. It asks whether there's any difference between smaller number and lower number, for which one of the biggest differences is in fact their relative prevalence. – FumbleFingers May 26 '11 at 13:20
  • @FubmleFingers: at least in a mathematician's POV, "lower" and "smaller" has no well-defined meaning; only less and greater has well defined meaning when comparing numbers. I'd personally suggest the OP to ask whoever wrote the sentence what they actually mean when they wrote that. – Lie Ryan May 26 '11 at 15:06
  • @Lie Ryan: That's just not true - "smaller" is used by mathematicians all the time. And "lower" is too, especially in the phrase lower bound. – psmears Jun 21 '11 at 08:25
  • 1
    Having looked again, I think an NGram for less than is totally irrelevant to OP's question, in that relatively few of the 'hits' will have anything to do with numbers. It remains the case that (for numbers, at least) smaller remains the comparator of choice, though semantically lower is equivalent. – FumbleFingers Jun 22 '11 at 00:57
  • @FumbleFingers: where have you been looking? Other than your own personal convictions and disbelief, how do you justify your belief that smaller is the comparator of choice? First you refused less than on the ground that it is rarely used outside the realm of mathematics, and now you accused that NGram results for less than is not about numbers; then how do you explain that less than is two orders of magnitude more prevalent than smaller number and an order of magnitude more than both smaller than and lower than? – Lie Ryan Jun 22 '11 at 09:40
  • @psmears: in those cases you pointed out, they are used for size/magnitude, which is always positive (therefore there are no confusion that can be caused by negative numbers). Although, I wouldn't be surprised that in a 3000 years old subject like mathematics there are people that abused the terms and misused terms that become popular (especially because most mathematicians does not dabble in language lawyering and terms and notations are abused all the time, for instance, there is nothing "real" about "real numbers", they aren't more or less real than any other types of numbers). – Lie Ryan Jun 22 '11 at 12:28
  • @Lie Ryan: After checking my own gut feeling (acquired from half a lifetime of exposure to usage, for which I can't meaningfully quote sources), I used Google to see what people write casually, then their book indexes to see what turns up in written publications. As I thought I already explained, less than is more prevalent as a 'general purpose' comparator (as opposed to more than). If you restrict the context to comparing numbers (as per my NGram), it's clear that smaller is overwhelmingly more common. – FumbleFingers Jun 22 '11 at 17:36
  • ...and just to make absolutely sure, I've checked for almost the exact form being asked about by OP, which I think must surely be accepted as evidence of usage, regardless of what anyone thinks about 'correctness'. – FumbleFingers Jun 22 '11 at 17:53
  • @FumbleFingers: as I previously said, people just don't use less number, it is redundant and wrong since less implies numbers (especially in mathematics, which I guess is the biggest consumers of numbers). While NGram is useful, it is a stupidly simple tool, when you add to the query the string number, you are not restrict the word's usage to the context of numbers (unlike regular google search), what it simply do is to add the string to the query. And because less number is redundant, it isn't a fairly setup playground. – Lie Ryan Jun 23 '11 at 01:31
  • @FumbleFingers: Another dataset taken from regular Google Search: less number has 2,600,000,000 results, lower number has 1,100,000,000 results, and smaller number has 570,000,000 results. – Lie Ryan Jun 23 '11 at 01:35
  • @LieRyan let us continue this discussion in chat – FumbleFingers Jun 23 '11 at 01:59
1

I believe my Calculus 2 prof used such terms as "more negative", "more positive", and "closer to zero", in case that's helpful. I know that doesn't answer the initial question. To answer that question: "smaller" is ambiguous for negative numbers, as http://en.wikipedia.org/wiki/Small_number points out; and I would suggest that "lower" is the same as "less than" but not popular for this particular phrase, getting used more in such general comparisons as "lower temperature".

Mathieu K.
  • 1,098
1

This confusion is the result of a semantic conflation. For positive numbers, magnitude covaries with value and "less than" is equivalent to "smaller," but this covariance is not valid for negative numbers. Negative numbers at a greater distance from zero are "less" than those at a smaller distance, mathematically speaking, but they are not "smaller." If mathematicians concur, then clarification in math texts and care on the part of math teachers may enable the problem to be solved in no more than a generation.

John Kuhl
  • 11