2

I'm sure I am overthinking this, but I wanted to understand this explanation better (and in turn, be able to explain it to students better). Observe the following explanation of a function in mathematics:

enter image description here

What it means to be a function f : A → B is this: f assigns to each element of A exactly one element of B. If a ∈ A, the notation f (a) denotes the element of B to which a is assigned by f.

I am unfamiliar with the usage of the phrase to which in the second sentence. when the author uses this phrase do they mean that the element a is assigned the element f(a) by f (in slightly different wording)?

Justin
  • 10,186
Taylor Rendon
  • 140
  • 3
    Ask yourself this: what does "which" (not "to which") refer to? – BillJ Jun 16 '22 at 13:23
  • @BillJ - In that case I would assume "which" refers to the element a previously mentioned at the beginning of the sentence? :) – Taylor Rendon Jun 16 '22 at 13:27
  • 2
    @TaylorRendon No, it refers to the element of B, the noun phrase that precedes it, which is called its Antecedent. The to originated in the phrase assigned to, and got moved to the front because which is its object. An equivalent way of saying it is the element of B which a is assigned by f to. That's pretty clunky, too, due to the passive is assigned to by f. If you want to look this up, the key phrase is "pied-piping". Honest. – John Lawler Jun 16 '22 at 13:55
  • @JohnLawler - Just so I understand your explanation and answer what I have asked above: according to what you've written, does this imply the author means that a is assigned the element f(a) (the element of B) by f? Thank you for your time, as well. – Taylor Rendon Jun 16 '22 at 13:59
  • 2
    Yes. It would have been easier if the author had used the active, thus making f's value the focus of the sentence. The passive puts it at the end, for unknown reasons. – John Lawler Jun 16 '22 at 14:06
  • 2
    I passed A-level maths (a long time ago, admittedly), but I must say I find OP's text "impenetrable", to say the least! So I'm guessing, but I suspect that last part is a clumsy way of saying ...f(a) is the element of B to which f assigns the value a. And I'm sure there are far less verbose ways of saying the same thing, anyway. – FumbleFingers Jun 16 '22 at 14:21

1 Answers1

2

This is a case where mathematics is assisted by precise English usage. I will tease it apart and try to illustrate with a specific example.

A is a set of elements.
B is a second set of elements.
f  is the name of a function that maps each element in A onto one of the elements in B.

In other words,  f  is the name of a defined operation by which we relate all elements of A to some (not necessarily all) of the elements of B.

Consider a simple example. I put all the elements as bold:

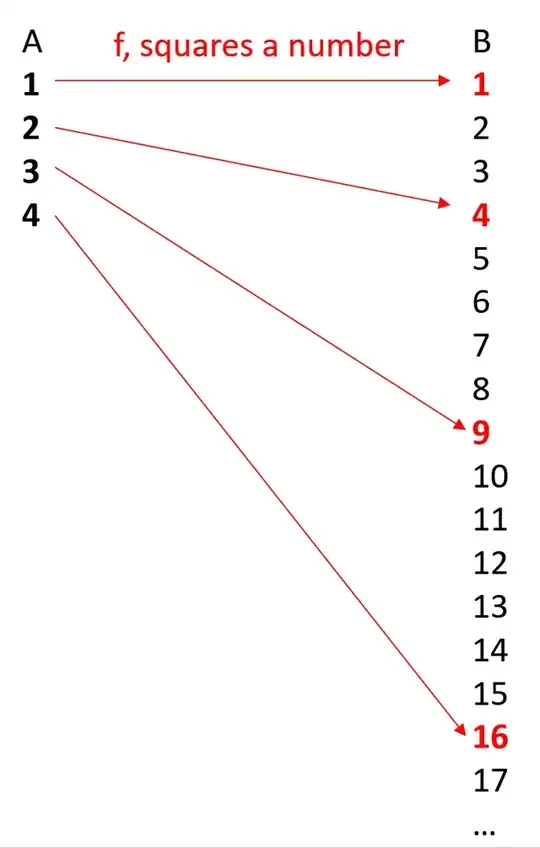
Let’s imagine A is the set {1, 2, 3, 4} and B is the set of all positive integers {1, 2, 3, 4, …}.

Now imagine  f  to be a function that maps any number onto its square.

So applying  f  to the set A {1, 2, 3, 4} → {1, 4, 9, 16}.

{1, 4, 9, 16} is a subset of B, and therefore every element of A is mapped to exactly one element of B.

Now consider the prose.

If a is a member of the set A, the operation f (a) means “map a to the corresponding element of B”.

In my example we would have  f (2) → 4.
4 is therefore the element of B referred to by  f (2).

Or, to put it as in your example, 4 is the element of B to which 2 is assigned by  f.

In an annotated version of the same statement:
4 [an element in B] is the element of B to which [referring to the relevant element in B] 2 [an element in A] is assigned by  f  [the mapping of a number to its square].

It may help if I illustrate the example with a picture:

enter image description here

Justin
  • 10,186
Anton
  • 28,634
  • 3
  • 42
  • 81